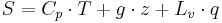Moist static energy
The moist static energy is a thermodynamic variable that describes the state of an air parcel, and is similar to the equivalent potential temperature.[1] The moist static energy is a combination of a parcels kinetic energy due to an air parcel's temperature, its potential energy due to its height above the surface, and the latent energy due to water vapor present in the air parcel. It is a useful variable for researching the atmosphere because, like several other similar variables, it is conserved during adiabatic ascent and descent.[2]
The moist static energy, S, can be described mathematically as:
where Cp is the specific heat at constant pressure, T is the absolute air temperature, g is the gravitational constant, z is the height above the surface, Lv is the latent heat of vaporization, and q is water vapor specific humidity.[3][4] Note that many texts use mixing ratio r in place of specific humidity q because these values tend to be close (within a few percent) under normal atmospheric conditions, but this is an approximation and not strictly correct.
Through the study of moist static energy profiles, Herbert Riehl and Joanne Malkus determined in 1958 that hot towers, small cores of convection approximately 5 kilometres (3.1 mi) wide that extend from the planetary boundary layer to the tropopause, were the primary mechanism that transported energy out of the tropics to the middle latitudes.[5] More recently, idealized model simulations of the tropics indicate that the moist static energy budget is dominated by advection, with shallow inflow in the lowest 2 kilometres (6,600 ft) of the atmosphere with outflow concentrated about 10 kilometres (33,000 ft) above the surface.[6] Moist static energy has also been used to study the Madden–Julian oscillation (MJO). As with the tropics as a whole, the budget of moist static energy in the MJO is dominated by advection, but also is influenced by the wind-driven component of the surface latent heat flux. The relationship between the advection component and the latent heat component influence the timing of the MJO.[7]
See also
References
- ^ American Meteorological Society (2000). "Moist static energy". AMS Glossary. http://amsglossary.allenpress.com/glossary/search?id=moist-static-energy1. Retrieved 25 June 2010.
- ^ University Corporation for Atmospheric Research (2010). "Adiabatic Processes and Vertical Distribution of Moisture". Introduction to Tropical Meteorology. http://www.meted.ucar.edu/tropical/textbook/ch6/moistprecip_6_2_3.html. Retrieved 25 June 2010. [Requires free registration]
- ^ Wallace, John; Peter Hobbs (2006). Atmospheric Science: An Introductory Survey (2nd ed.). Elsevier. ISBN 0-12-732951-X.
- ^ Maloney, Eric D. (2009). "The Moist Static Energy Budget of a Composite Tropical Intraseasonal Oscillation in a Climate Model". Journal of Climate 22 (3): 711–729. Bibcode 2009JCli...22..711M. doi:10.1175/2008JCLI2542.1.
- ^ Riehl, Herbert; Malkus, Joanne (1958). "On the heat balance in the equatorial trough zone". Geophysica 6 (3–4).
- ^ Powell, S.W.; Nolan, D.S.. "Calculating the moist static energy budget around the ITCZ in idealized WRF simulations". Seventh Annual AMS Student Conference. http://ams.confex.com/ams/88Annual/techprogram/paper_136910.htm.
- ^ Maloney, Eric D. (2009). "The Moist Static Energy Budget of a Composite Tropical Intraseasonal Oscillation in a Climate Model". Journal of Climate 22 (3): 711–729. Bibcode 2009JCli...22..711M. doi:10.1175/2008JCLI2542.1.